Find Critical Value of Z
In this article, we will discuss what is the critical value of z and when to use the critical value of z.
We will discuss critical value z for the left-tailed test, a right-tailed test, and a two-tailed test on TI 84 with examples.
What is critical value or Significant Value?
The value of the test statistic which separates the critical (or rejection) region and the acceptance region is called the critical value or significant value. It depends on the:
- The level of significance used, and
- The alternative hypothesis used whether it is two-tailed or one-tailed.
The critical Value is like a cut-off value (or two cut-off values in the case of the two-tailed test) that divides the area under the probability distribution curve in rejection region(s)and non-rejection region(s).
Once we get the rejection region, then identify the value of the test statistic belonging to it.
If the test statistic belongs to the rejection region, then we can reject the null hypothesis and accept the alternative hypothesis
If the test statistic does not belong to the rejection region, then we do not have enough evidence to reject the null hypothesis.
Critical value depends upon the alternative hypothesis you choose for your test i.e. it is a one-tailed or two-tailed test.
The following three graphs show a left-tailed test, a right-tailed test, and a two-tailed test.
We have considered the idealized model, thus the null hypothesis H0 is described by a bell-shaped normal probability curve.
How to find the critical value of z?
When the sample distribution is normal, the critical value can be expressed in two ways: z score related to cumulative probability or t score, depending upon the sample size.
Critical Value is used to calculate the margin of error within a data set in order to determine the validity of the data.
The following steps will guide how to calculate the critical value of Z.
1. Compute the alpha value ( i.e. level of significance (α) )
Alpha Value (α) = 1- (confidence level /100)
In case of a 95% Confidence level, the alpha is computed as :
Alpha Value (α) = 1-(95/100) = 1-0.95 = 0.05
the alpha value = 0.05
2. Compute the critical probability (p)*
Critical Probability(p*) = 1- (α/2)
3. Find the critical z-score corresponding to the critical probability from z-table
To express the critical value as a z-score, find the z-score having a cumulative probability equal to the critical probability (p*) from the z-table
Critical Value Z table for Various Confidence Levels:
| Confidence Level | Significance Level α | Two-Tailed Z-Critical Value | Left-Tailed Z-Critical Value (One-tailed) | Right-Tailed Z-Critical Value (One-tailed) |
|---|---|---|---|---|
| 80% | 0.20 | 1.282 | -0.8416 | 0.8416 |
| 85% | 0.15 | 1.439 | -1.036 | 1.036 |
| 90% | 0.10 | 1.645 | -1.282 | 1.282 |
| 95% | 0.05 | 1.960 | -1.645 | 1.645 |
| 97% | 0.03 | 2.17 | -1.881 | 1.881 |
| 98% | 0.02 | 2.326 | -2.0537 | 2.0537 |
| 99% | 0.01 | 2.576 | -2.326 | 2.326 |
| 99.5% | 0.005 | 2.807 | -2.576 | 2.576 |
| 99.8% | 0.002 | 3.090 | -2.807 | 2.807 |
| 99.9% | 0.001 | 3.291 | -3.090 | 3.090 |
How to Find critical value z on a TI-84 calculator
While performing the hypothesis test, we get a test statistic as an output.
In order to make a decision about whether the results of the hypothesis test are statistically significant or not, we need to compare the test statistic to a Z critical value.
If the absolute value of the test statistic is greater than the Z critical value, then the results of the test are statistically significant.
To find the Z critical value on a TI-84 calculator, we will use the Inverse Normal Probability Distribution Function invNorm().
invNorm(probability, μ, σ)
where:
probability: the level of significance (α) μ: population mean σ: population standard deviation
The following steps will guide how to calculate the critical value of Z on the TI-84 Calculator:
Step 1: Press “2nd” and then press “VARS”.This will take you to a DISTR screen.
Step 2: Now, select “invNorm” i.e. 3rd option, and then press “ENTER” to bring up the invNorm wizard screen.
Step 3: Enter the desired percentile as a decimal next to the word area followed by 0 for mean and 1 for standard deviation. For example, to find the z-score associated with the level of significance of 0.05 then, type 0.05,0,1.
Step 4: Type a closing parenthesis “)” and then press ENTER.
The TI-84 Plus will calculate the z-score associated with the given level of significance.
Let’s understand with an example to find the critical value of z on TI 84.
Cool Tip: How to find an area to the left for the given z
How to Find critical value z for a left-tailed Test on TI-84
Find the critical value z for a left-tailed test with a significance level of 0.05.
We will solve this example with step by step procedure.
- Press “2nd” and then press “VARS”.This will display the “DISTR” screen.
- Select “invNorm” i.e 3rd option, and then press “ENTER” to bring up the invNorm wizard screen.
- Type 0.05,0,1
- Type a closing parenthesis “)” and then press ENTER.
- The resultant z-score for the left tail is -1.6449
Conclusion:
If the test statistic of the performed hypothesis test is less than -1.6449, then the results of the test are statistically significant at α = 0.05.
Cool Tip: How to find the area between the two z-scores
Find critical value z for a right-tailed test on TI-84
Find the critical value z for a right-tailed test with a significance level of 0.01.
We will solve this example with a step-by-step procedure.
- Press “2nd” and then press “VARS”.This will display the “DISTR” screen.
- Select “invNorm” i.e. 3rd option, and then press “ENTER” to bring up the invNorm wizard screen.
- Type 1-0.01,0,1
- Type a closing parenthesis “)” and then press ENTER.
The resultant z-score for the right tail is 2.326
Conclusion:
If the test statistic of the performed hypothesis test is greater than 2.326, then the results of the test are statistically significant at α = 0.01.
Cool Tip: How to calculate z-score in R
How to Find critical value z for a two-tailed test on TI-84
Find the critical value z for a right-tailed test with a significance level of 0.05.
We will solve this example with a step-by-step procedure.
- Press “2nd” and then press “VARS”.This will display the “DISTR” screen.
- Select “invNorm” i.e. 3rd option, and then press “ENTER” to bring up the invNorm wizard screen.
- Type 0.05/2,0,1
- Type a closing parenthesis “)” and then press ENTER.
The resultant z-score for the right tail is -1.96,1.96
Conclusion:
Since this is a two-tailed test, we get two critical values: -1.96 and 1.96.
If the test statistic of the test is less than -1.96 or greater than 1.96, then the results of the test are statistically significant at α = 0.05.
Cool Tip: How to calculate one-sample z-test in R!
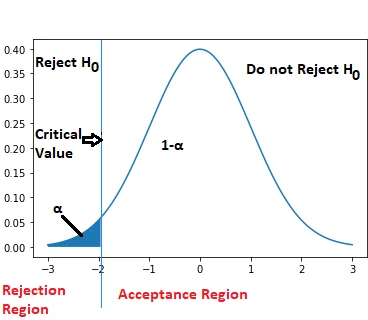
Left tailed test
In a left-tailed test, the null hypothesis is rejected if the test statistic is too small.
The rejection region for such a test consists of one part of the curve, which is left from the center with an area equal to α, as shown below.
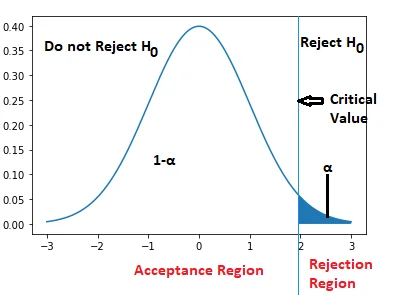
Right tailed test
In a right-tailed test, the null hypothesis is rejected if the test statistic is too large.
The rejection region for such a test consists of one part of the curve, which is right from the center with an area equal to α, as shown below.
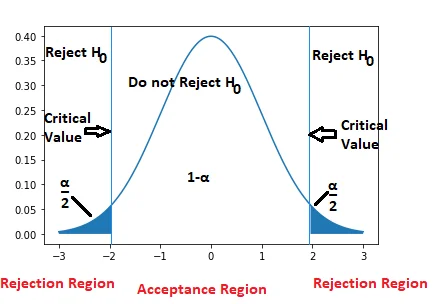
Two-tailed test
In a two-tailed test, the null hypothesis is rejected if the test statistic is either too small or too large.
The rejection region for such a test consists of two parts of the curve: one on the left and one on the right from the center with an area equal to α/2 on both sides.
Conclusion
I hope the above article on how to find critical value z for left-tailed, right-tailed, and two-tailed tests is helpful to you.
The critical value is used in hypothesis testing to determine whether the sample statistics are significant or not.
We have learned in different examples to find the critical z value for the test on Ti 84.
Cool Tip: How to transform a set of raw scores into a set of z-scores!
You can find more topics about Z-Score and how to calculate the z-score given the area on the ZscoreGeek home page.