How to Find Percentiles from Z-Score on TI-84
The Normal Cumulative Distribution Function normalcdf() is used to find percentiles from the z score on the TI-84 calculator.
normalcdf
(lower bound, z-score, μ, σ)
where:
- lower bound: lower bound for the given z-score. We use infinity as a lower bound.
- Z-score: given z-score
- μ: population mean
- σ: population standard deviation
How to find percentile from z score using TI 84
The following steps will guide us on how to calculate the Percentiles from Z-Score using TI-84 Calculator:
-
Step 1: Press “2nd” and then press “VARS”.This will take you to a DISTR screen.
-
Step 2: Now, select “normalcdf“ i.e. 2nd option, and then press “ENTER” to open the normalcdf wizard screen.
-
Step 3: Enter the lower bound, z-score followed by 0 for mean and 1 for standard deviation.
For example, to find the Percentiles for a z-score of 1.2 on the TI-84 calculator,
type -1000,1.2,0,1. Here the lower bound is infinity, so type -1000.
Always use large numbers to represent infinity, like -1000 in this case.
- Step 4: Type a closing parenthesis “)” and then press ENTER.
The TI-84 Plus will calculate the percentile associated with the given z-score.
Let’s discuss a few examples to find percentiles from the Z-score on TI-84.
How to find the Percentile of Negative Z-score on TI-84?
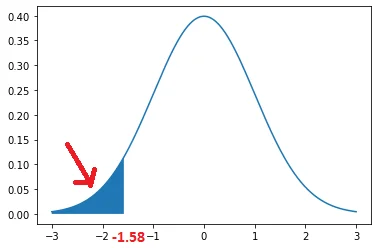
Let’s consider an example to find the percentile from z score -1.58 on the TI-84 calculator
The following steps will guide us on how to calculate the Percentiles from Z-Score = -1.58 Using the TI-84 Calculator
Let’s draw the normal distribution curve for the given z-score = -1.58
-
Step 1: Press “2nd” and then press “VARS”.This will take you to a DISTR screen.
-
Step 2: Select “normalcdf“ i.e. 2nd option, and press “ENTER” to bring up the normalcdf wizard screen.
-
Step 3: Enter the lower bound, z-score followed by 0 for mean and 1 for standard deviation. In this case, type -1000,-1.58,0,1.
Note: Here the lower bound is infinity, so type -1000.
- Step 4: Type a closing parenthesis “)” and then press ENTER.
The TI-84 Plus will calculate the percentile associated with the given -1.58 z-score.
The resultant percentile for the given z-score = -1.58 is 0.0571.
Conclusion: It concludes that 5.71% of the data values in the standard normal distribution lies below the z-score of -1.58.
Cool Tip: How to Calculate Z Score in Excel!
How to find the Percentile of Positive Z-score on TI-84?
Let’s consider an example to find the percentile from z score 0.31 on the TI-84 calculator.
The following steps will guide how to calculate the Percentiles from Z-Score = 0.31 on TI-84 Calculator:
-
Step 1: Press “2nd” and then press “VARS”.This will take you to a DISTR screen.
-
Step 2: Select “normalcdf“ i.e. 2nd option, and then press “ENTER” to bring up the normalcdf wizard screen.
-
Step 3: Enter the lower bound, z-score followed by 0 for mean and 1 for standard deviation. In this case, type -1000,0.31,0,1.
Note: Here the lower bound is infinity, so type -1000.
- Step 4: Type a closing parenthesis “)” and then press ENTER.
The TI-84 Plus will calculate the percentile associated with the given 0.31 z-score.
The resultant percentile for the given z-score = 0.31 is 0.6217.
Conclusion: It concludes that 62.17% of the data values in the standard normal distribution lies below the z-score of 0.31.
Cool Tip: Read more here about how to use a z-score calculator!
Conclusion
I hope the above article to find percentile from z score on the TI-84 calculator is useful to you.
In the above article, we have learned how to find the percentile from a negative z score on a TI-84 calculator and find the percentile from a positive z score on the TI-84 calculator.
Normal Cumulative Distribution function normalcdf() function is used to find the percentile for a given z score on the TI-84 calculator.
Cool Tip: Read more about how to find the z score from percentile on the Ti-84 plus calculator!
You can find more topics about Z-Score and how to calculate z score given the area on the ZscoreGeek home page.