Find the Area between Two Negative Z Scores

The area between two negative scores can be found by finding the area between two z-score and subtracting the small area from the larger area.

The Z-Score table represents the area under the normal curve for a normal distribution.

In this article, we will discuss how to find the area between two negative z scores on one side of the mean with an example.

The Area between two negative Z Scores

To find the area between two negative z-scores, let’s understand with an example.

Consider, that you have z scores of -0.45 and -0.95 and you want to find the area between these two negative z scores.

These z-scores are negative hence we will use a negative z-score table chart.

Follow the below steps to find the area between two negative z scores

• Step 1: Two Z-Score values are -0.45 and -0.95

• Step 2: Use the negative z score table to find the area for each z score.

• Step 3: Find the area for -0.45

Use the negative z-score table to find the area. Look for -0.4 in the left column and 0.05 in the row, the intersection between these two is 0.3264.

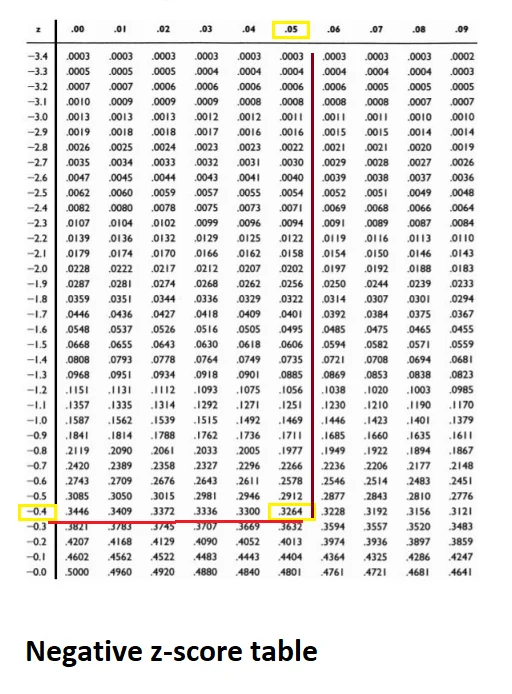
• Step 4: Find the area for -0.95

Use the negative z score table to find the area. Look for -0.9 in the left column and 0.05 in the row, the intersection between these two is 0.1711.

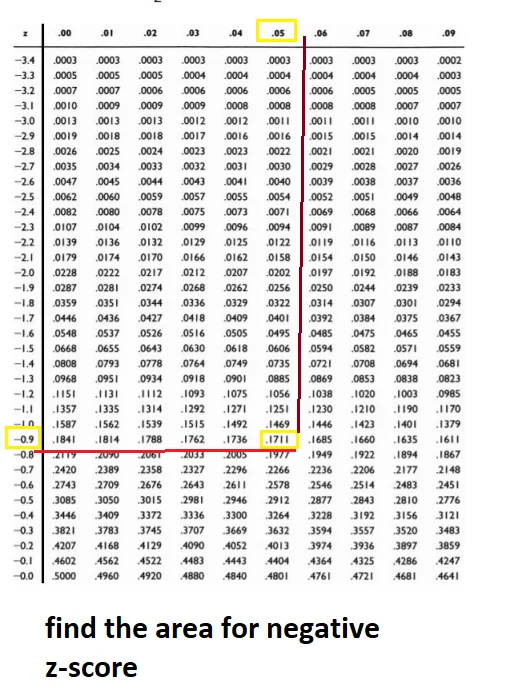
• Step 5: Subtract the smaller area from the larger area

In steps 3 and step 4, we find the areas for two negative z-scores as 0.3264 and 0.1711

To find the area between two negative z scores, subtract the smaller area from the larger area as given below

= 0.3264 – 0.1711

= 0.1553

The resultant 0.1553 is the area between the two negative z scores.

Z-Score Tip: How to find the area between two z-scores of opposite sides of the mean!

Conclusion

I hope the above article on how to find the area between two negative z scores on one side of the mean is helpful to you.

You can find more topics about Z-Score and how to calculate the z score given the area on the ZscoreGeek home page.