Find the Area under Standard Normal Curve to the right of Z
In this article, we will discuss step by step guide on how to find the area under the standard normal curve to the right of the z score.
The area under the Standard Normal Curve to the right of Z
Step to find the area under the standard normal curve to the right of z
-
Step 1: Find the area to the left of z.
-
Step 2: As the total area under the bell curve is 1.
-
Step 3: Subtract the area to the left from 1.
area to the right of z = 1 – area to the left of z.
- Step 4: Multiply it by 100 to calculate the percentage of area.
Let’s understand to find the area under the standard normal curve to the right of z using an example.
Z-Score Tip: Read more on how to calculate z score!
How do you find the area to the right of z = 0.52
To find the area to the right of given z follow the below steps:
Step 1: Find the area to the left of Z
To find the area to the left of the given z follow the below steps:
-
Choose a positive z-table as the given z-score (i.e 0.52) is positive.
-
Check the area value for the given z in the z-table.
-
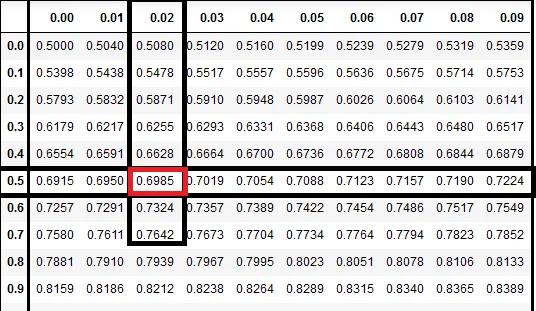
Look at the first two digits(0.5) of the z-score on the left side column (y-axis) of the z-table and then the remaining number (0.02) on the x-axis on the topmost row.
-
The intersection of the two is 0.6985 (highlighted in red).
-
area to the left = 0.6985
Step 2: The total area under the bell curve is 1
Step 3: Subtract the area to the left from 1
area to the right of z = 1 – area to the left of z.
The area under the standard normal curve to the right of z = 1 – 0.6985 = 0.3015
Step 4: Multiply it by 100 to calculate the percentage of area.
area to the right of z = 0.3015*100 = 30.15%
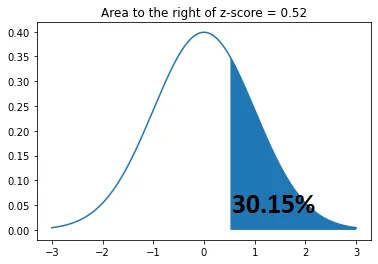
Result: Result: The area to the right of z is 30.15% of the normal standard curve.
Z-Score Tip: Read more on how to Calculate Z Score in Excel!
Conclusion
I hope the above article to find the area under the standard normal curve to the right of z using step by step guide is helpful to you.
You can find more topics about Z-Score and how to calculate z score given the area on the ZscoreGeek home page.