How to Find Z Score on TI-84 plus Calculator
The Inverse Normal Probability Distribution Function invNorm() is used to find z score from the percentile on TI-84 plus calculator.
invNorm(probability, μ, σ)
where:
- probability: the given percentile
- μ: population mean
- σ: population standard deviation
Note: Finding the Z-score indicates that the given distribution is a standard normal distribution with a mean of 0 and a standard deviation as 1.
Using the invNorm function on TI 84 plus
The following steps will guide us on how to calculate the Z-Score from Percentile on TI-84 plus Calculator:
-
Press “2nd” and then press “VARS”.This will take you to a DISTR screen.
-
Select “invNorm” i.e 3rd option, and then press “ENTER” to bring up the invNorm wizard screen.
-
Enter the desired percentile as a decimal next to the word area followed by 0 for mean and 1 for standard deviation. For example, to find the z-score associated with the 95th percentile, type 0.95,0,1.
-
Type a closing parenthesis “)” and then press ENTER.
Using the TI-84 Plus calculator will calculate the z-score associated with the given percentile.
Let’s discuss a few examples to find the z score on TI-84 plus ce
Find the Z Score corresponding to the 1st Quartile using TI-84
The 1st Quartile represents the 25th percentile in the normal distribution.
Let’s first draw the normal distribution curve for percentile = 0.25
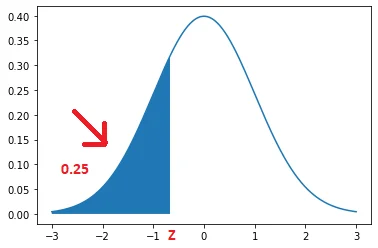
The following steps will guide how to calculate the z score corresponding to the 1st Quartile on TI-84 plus Calculator:
-
Press “2nd” and then press “VARS”.This will display the “DISTR” screen.
-
Select “invNorm” i.e 3rd option, and then press “ENTER” to bring up the invNorm wizard screen.
-
Type 0.25,0,1
-
Type a closing parenthesis “)” and then press ENTER.
The resultant z-score for the left tail is -0.67.
Conclusion: The Z-score associated with the 1st Quartile in the normal standard distribution is -0.67.
Cool Tip: How to on find percentile from z score the TI-84 calculator!
Find Z-Scores for the top 20th Percentile on TI-84
The top 20% of the normal distribution indicates that only 20% of the data lies on the right of the normal standard curve.
Let’s first draw the normal distribution curve for the top 20th percentile.
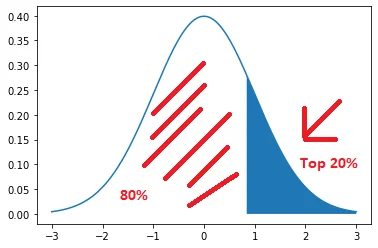
The minimum percentile required left to the required z-score is 80% i.e. (100-20)%.
The invNorm takes the probability of values less than the required z-score. So, we will check the 0.80 probability in order to calculate the top 20% of the distribution.
To find the z-score for the 80 percentile, we will follow the below steps:-
The following steps will guide you on how to calculate the Z-Scores for the top 20th Percentile on TI-84 Calculator:
-
Press “2nd” and then press “VARS”.This will display the “DISTR” screen.
-
Select “invNorm” i.e 3rd option, and then press “ENTER” to bring up the invNorm wizard screen.
-
Type 0.80,0,1
-
Type a closing parenthesis “)” and then press ENTER.
The resultant z-score is 0.8416.
Conclusion: The Z-score associated with the top 20th Percentile in the normal standard distribution is 0.8416.
Cool Tip: How to Calculate Z Score in Excel!
Conclusion
I hope the article on how to find the z score on TI-84 plus calculator is useful to you.
invNorm (Inverse normal distribution) function is used to calculate the z score from the percentile on the TI-84 calculator.
You can find more topics about Z-Score and how to calculate z score given the area on the ZscoreGeek home page.