Z Score Table and Chart (How to use Z-Score)

Z table or the Z-score table also called the standard normal table is a mathematical table used to find the probability that the z-score value is below, above, or between the values on the standard normal distribution.

Standard scores are most commonly called z-scores. In this post, equivalent terms like z-values, standardized variables, and normal scores are used.

The standard normal distribution table is the normal distribution having a mean value of 0 and a standard deviation of 1.

The standard score value gives you how far the raw score value is from the mean.

The Z-score value either be Positive or Negative depending on raw score value is greater than the mean or less than the mean.

The positive Z score value represents the raw score value is higher than the mean of the distribution. Use the Z score table pdf file to determine the corresponding area or probability to a positive z score value.

For example, the z-score value of 2 indicates it is 2 standard deviations greater than the mean.

A negative Z score value indicates the raw score value is below the mean of the distribution. Use the negative z table pdf file to determine the probability of a negative z score value.

Positive Z Score Table

Use the standard normal distribution table or z table chart to find values on the right of the mean distribution.

Corresponding values are higher than the mean of the distribution.

The positive z score in the z-table represents the area under the bell curve to the right of z.

Negative Z Score Table

Use the Negative Z score table or Z table chart to find values on the left of the mean distribution in the following z table.

Corresponding values are less than the mean of the distribution. The negative z score in the z-table represents the area under the bell curve to the left of z.

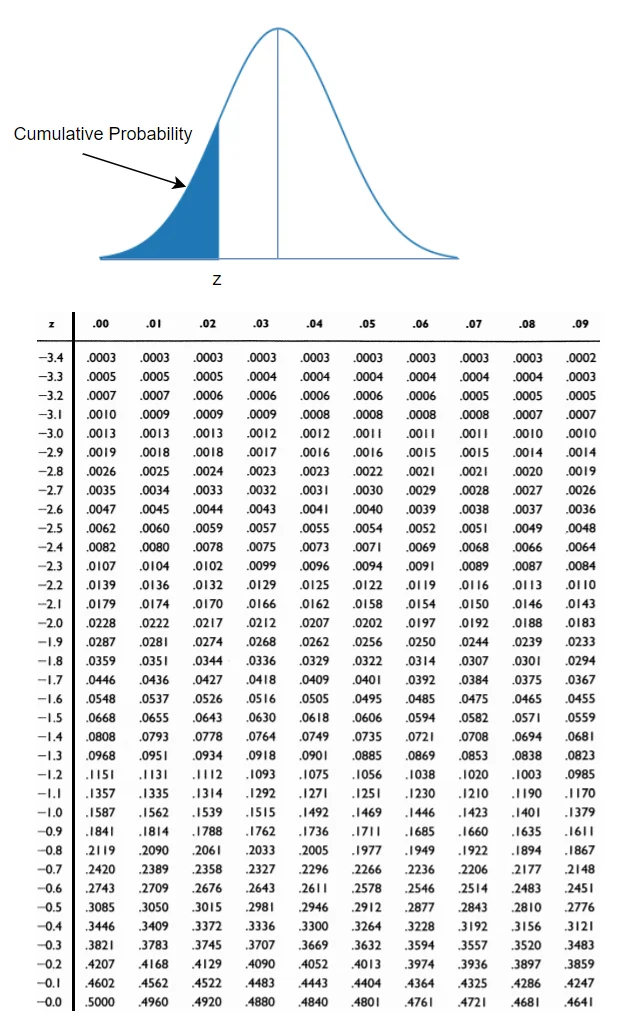
How to read Z Table

Z table is used to find the z score value lies on the left of the mean or right of the mean distribution.

To use the Z table, you should have a Z score value.

You can refer Z score calculator article which explains how to calculate the Z score using the z score formula below

z = (x -μ )/σ

Where: μ = is the population mean for the unstandardized value σ = is the population standard deviation for the unstandardized value x = is the raw score value

z = is the calculated z-score value.

If the z score value is positive, use the positive z table to find the area on the right of the mean of the distribution.

If the z score value is negative, use the negative z table to find an area on the left of the mean of the distribution.

Let’s consider an example to find the z score value and corresponding probability.

We have below the inputs parameter

The mean of the population for the unstandardized value = 75

The population standard deviation for the unstandardized value = 15

Raw Score Value: 83

Using the above input values as per the Z score formula, it calculates the Z score value below

Z score = (83 – 75)/15 Z = 0.54

Now as we have the Z score value, use the z table chart.

The z score value is positive hence we will use the positive z table chart to find an area on the right of the mean.

To find a z-score using the table, look up the z-score value on the positive z-score table.

Find the first two digits of the z score to map it on the Y-axis of the normal distribution table, in our case first, two digits are 0.5

Find the value of digits at the second decimal position in z score value, it is 0.04

In the below z table, the yellow color box indicates the mapping of the z score value on the Y-axis and X-axis to find the corresponding area as marked in red color

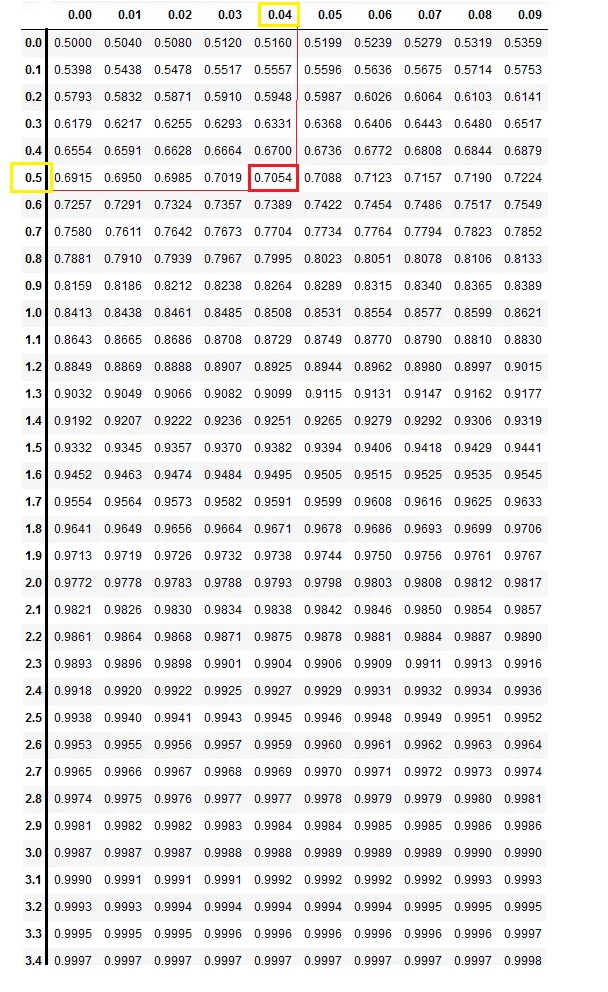
The corresponding area is 0.7054 which means 70.54%

For the normal standard curve, what percent of the data values are below the third quartile denoted by Q3, and also find the z-score corresponding to Q3?

We know the Q3 Quartile represents the 75th percentile in the standard normal distribution.

It means there 75% of the data values lies below the third Quartile in the standard normal distribution.

Let’s first draw the normal distribution curve for percentile = 0.75

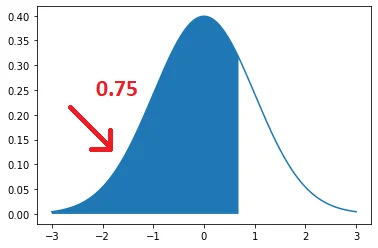
To find the z-score for the 75th percentile, we will follow the below steps

Step-1

Go to the z score chart and check the probability closest to 0.75 in the values inside the table.

Sometimes the exact values do not exist, in that case, we will consider the best closest value.

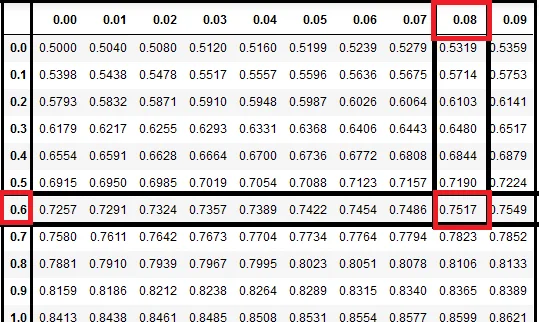
The closest value in the Z-table is 0.7517

Step-2

Find the z-score corresponding to this value i.e in this case its corresponding row value is 0.6 and its corresponding column value is 0.08

Step-3

Combine these numbers as 0.6+0.08 = 0.68

Conclusion

The Z-score for the Q3 Quartile is 0.68 which means 75% of the data point of the normal distribution is below 0.68 z-score.

Z-Score Percentile Table for Normal Distribution

The below table displays the z-score percentile table for the standard normal table

Percentile	Z-Score
5	-1.645
10	-1.282
20	-0.842
40	-0.253
50	0
60	0.253
80	0.842
85	1.036
90	1.282
95	1.645
97	1.881
98	2.054
99	2.326

Z Score Percentile Table for Normal Distribution

Z Value Table for Confidence Intervals

To find the z score for the confidence intervals, use the below table.

Confidence Interval ((1–α) * 100%)	Significance level (α)	Critical Z-Value (Z-score)
80%	0.20	1.282
85%	0.15	1.439
90%	0.10	1.645
95%	0.05	1.960
97%	0.03	2.17
98%	0.02	2.326
99%	0.01	2.576
99.5%	0.005	2.807
99.8%	0.002	3.090
99.9%	0.001	3.291

What’s the difference between Z-Score vs Percentile?

Z-Score:

• Z-score measures how much a z-score deviates from the mean of the distribution in terms of standard deviation.
• It tells us about the position of the data value in the normal distribution.
• It describes the distance between two extreme data points in the distribution very accurately.
• Z-score ranges from −∞ to ∞
• It can be used only in the case of normal distribution.

Percentile:

• The Percentile indicates the percentage of data values lies below the certain z-value in the distribution.
• It only tells us about the fraction of data values lies below the data value but does not specify their positions in the distribution.

Z Score Table Pdf

You can download the z score table pdf file having the positive z score chart and negative z score chart in pdf file from given below link.

Cool Tip: How to Calculate the Z Score in Excel!

Z Table Chart FAQ

What is the z table in normal distribution?

Z-table also called a standard normal table shows the percentages of values to the left of the given z score on the standard normal distribution.

How to read z table chart?

z-table tells us the probability of values less than the given z-score.

To find the probability of values less than the given z-score using z score chart, follow the below steps:

Step 1: Check the first two digits i.e. one digit and the first digit after the decimal point then go to the column on the left side(on the leftmost y-axis) and find the row corresponding to your z-score.

Step 2: Now, go to the x-axis present on the topmost row, check the remaining number i.e the second digit after the decimal point(hundredth place digit), and find the column corresponding to your z-score.

Step 3: The intersection of the two (Step 1 & Step 2) will lead to results.

Finally, we get the P(Z<z) i.e the probability of random variable Z less than the given z value.

What are the Types of Z Score Tables?

There are two types of tables depending on the z-score.

Positive z-score table: It is used when the z-score is positive or when the z-score is above the mean.

Negative z-score table: It is used when the z-score is negative or when the z-score is below the mean.

What does the Z-Score Table tell?

A z-score table tells us the probability of values that exists above or below the given z-value. It gives the area under the normal standard curve left to the given z-score.

Negative z-scores indicate that the values are less than the mean and Positive Z-scores indicate the values are greater than the mean of the normal distribution.

Why use a z-table and How to use z table chart?

The z-table helps to calculate the percentage of the observations below (to the left) a given z-score in a standard normal distribution.

When you want to compare two or more sets of data that have a normal distribution but different means and standard deviations, it’s difficult to compare.

Using standardizing the raw score data, it calculates the z-score value.

When we use a value from the original data points and calculate its z score, we basically standardized that data value from the original distribution to a standard normal distribution with a mean of 0 and standard deviation of 1.

Since this formula works for every data set with a normal distribution, it makes comparisons easy between data sets having different parameters.

To use the z-score chart, however, you will need the z-score. It is usually either pre-provided or has to be calculated using the z-score formula.

Is a higher z-score better?

A higher z-score tells us that the data value is too many standard deviations away from the mean.

In many scenarios, a higher z-score is always better in order to get good results.

For example, a higher z-score is always better while evaluating the exam results. A higher z-score indicates higher percentiles.

John secured marks of z-score = 1.90 with 97.13% percentile & Jack secured marks of z-score = 2.10 with 98.21% percentile.

In the above example, Jack secured good marks as compared to John. A higher z-score indicates a higher percentile.

Which z score is more extreme, 0.68 or -0.92?

When comparing z-scores, the more extreme z-score is the one that is far away from the mean.

In this case, the z-score of 0.68 is positive, which means its value is greater than the mean. While the z-score of -0.92 is negative, which means its value is below the mean.

Hence, a z-score for -0.92 is more extreme as it is far away from the mean as compared to z-score for 0.86

Conclusion

I hope the above article about how to use the Z table to find a corresponding area or cumulative probability using the positive z table or negative z score table chart is helpful to you.

Z score computation requires information about mean and standard deviation.

A Z score chart is called a standard normal table used to calculate the area under the normal bell curve.

To find the corresponding area, you will need a z score value which can be calculated using the z score formula or you can use our z score calculator to find the z score value.

You can find more topics about Z-Score and how to calculate the z score given the area on the ZscoreGeek home page.